Derivative Of 1 X Easy 1 X Rule Application
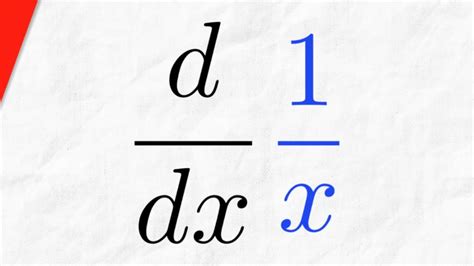
In calculus, finding the derivative of a function is a fundamental operation that helps us understand how the function changes with respect to its input variable. One of the most basic and frequently used rules for differentiation is the Power Rule. However, when dealing with functions like ( \frac{1}{x} ), a slight modification of this rule is necessary. Let’s explore the derivative of ( \frac{1}{x} ) using the Power Rule and understand its application step by step.
Understanding the Function ( \frac{1}{x} )
The function ( \frac{1}{x} ) can be rewritten as ( x^{-1} ). This form is crucial because it allows us to directly apply the Power Rule, which states:
[ \frac{d}{dx}(x^n) = nx^{n-1} ]
Here, ( n = -1 ). Substituting ( n ) into the Power Rule:
[ \frac{d}{dx}(x^{-1}) = -1 \cdot x^{-1-1} = -x^{-2} ]
Thus, the derivative of ( \frac{1}{x} ) is:
[ \frac{d}{dx}\left(\frac{1}{x}\right) = -\frac{1}{x^2} ]
Step-by-Step Application of the Power Rule
- Rewrite the function: Express ( \frac{1}{x} ) as ( x^{-1} ).
- Identify the exponent: Here, ( n = -1 ).
- Apply the Power Rule: Multiply the exponent by the coefficient (which is implicitly 1 in this case) and reduce the exponent by 1.
[ \frac{d}{dx}(x^{-1}) = -1 \cdot x^{-2} ]
- Simplify the result: Write ( x^{-2} ) as ( \frac{1}{x^2} ).
[ -x^{-2} = -\frac{1}{x^2} ]
Why This Works: The Power Rule in Depth
The Power Rule is derived from the definition of the derivative and the binomial theorem. For any constant ( n ), the derivative of ( x^n ) is:
[ \frac{d}{dx}(x^n) = \lim_{h \to 0} \frac{(x+h)^n - x^n}{h} ]
Using the binomial expansion for ( (x+h)^n ), we can simplify this limit to ( nx^{n-1} ). For ( n = -1 ), this process yields:
[ \frac{d}{dx}(x^{-1}) = -x^{-2} ]
Practical Example: Applying the Rule
Consider the function ( f(x) = \frac{1}{x^2} ). Rewriting it as ( x^{-2} ), we apply the Power Rule:
[ f’(x) = -2x^{-3} = -\frac{2}{x^3} ]
This demonstrates how the Power Rule extends to more complex expressions involving negative exponents.
Common Mistakes to Avoid
- Forgetting the negative sign: The derivative of ( x^{-1} ) is ( -x^{-2} ), not ( x^{-2} ).
- Misapplying the rule: Ensure the function is in the form ( x^n ) before applying the Power Rule.
- Confusing with the reciprocal rule: While ( \frac{1}{x} ) is a reciprocal, the Power Rule directly applies here.
Historical Context: The Power Rule
The Power Rule was formalized by Isaac Newton and Gottfried Wilhelm Leibniz in the late 17th century as part of their development of calculus. It remains one of the most widely used rules in differentiation due to its simplicity and broad applicability.
Future Implications: Beyond Simple Functions
Understanding the derivative of ( \frac{1}{x} ) lays the groundwork for more advanced topics, such as:
- Rational functions: Derivatives of functions like ( \frac{2x+1}{x^2} ).
- Chain Rule applications: Differentiating composite functions involving ( \frac{1}{x} ).
- Integration techniques: Using the derivative to find antiderivatives of related functions.
FAQ Section
What is the derivative of \frac{1}{x^3} ?
+Rewrite \frac{1}{x^3} as x^{-3} . Applying the Power Rule: \frac{d}{dx}(x^{-3}) = -3x^{-4} = -\frac{3}{x^4} .
Can the Power Rule be used for non-integer exponents?
+Yes, the Power Rule applies to any real number exponent n , including fractions and decimals.
Why is the derivative of \frac{1}{x} negative?
+The negative sign arises from the exponent -1 in the Power Rule: -1 \cdot x^{-2} = -\frac{1}{x^2} .
How does this relate to the quotient rule?
+While the quotient rule can be used for \frac{1}{x} , the Power Rule is simpler and more direct for this specific case.
Key Takeaway
The derivative of \frac{1}{x} is -\frac{1}{x^2} , derived using the Power Rule. This rule is a cornerstone of calculus, enabling the differentiation of a wide range of functions with minimal effort.
By mastering this concept, you’ll be better equipped to tackle more complex problems in calculus and beyond.



