Cramers Rule Calculator Finds Solutions Easily
In the realm of linear algebra, solving systems of linear equations is a fundamental task that arises in numerous applications, from engineering and physics to economics and computer science. One of the classical methods for solving such systems is Cramer’s Rule, a deterministic approach that provides an explicit formula for the solutions in terms of determinants. While it may not be the most computationally efficient method for large systems, Cramer’s Rule offers a clear, analytical solution that is invaluable for understanding the underlying mathematics. With the advent of digital tools, implementing Cramer’s Rule has become more accessible, and a Cramer’s Rule Calculator emerges as a powerful utility for students, educators, and professionals alike.
Understanding Cramer’s Rule
Before delving into the calculator, it’s essential to grasp the basics of Cramer’s Rule. Consider a system of n linear equations in n variables:
[ \begin{cases} a_{11}x1 + a{12}x2 + \cdots + a{1n}x_n = b1 \ a{21}x1 + a{22}x2 + \cdots + a{2n}x_n = b2 \ \vdots \ a{n1}x1 + a{n2}x2 + \cdots + a{nn}x_n = b_n \end{cases} ]
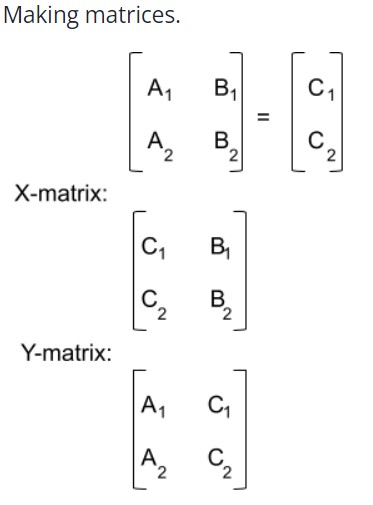
Cramer’s Rule states that if the determinant of the coefficient matrix ( D = \det(A) ) is non-zero, then the system has a unique solution, and each variable ( x_i ) can be found using the formula:
[ x_i = \frac{D_i}{D} ]
where ( D_i ) is the determinant of the matrix obtained by replacing the i-th column of ( A ) with the column vector ( \mathbf{b} ).
The Role of a Cramer’s Rule Calculator
A Cramer’s Rule Calculator automates the process of applying Cramer’s Rule, eliminating the need for manual determinant calculations, which can be tedious and error-prone, especially for larger systems. Here’s how such a calculator typically operates:
- Input the System: Users input the coefficients of the system and the constants on the right-hand side. This can be done through a matrix interface or individual entry fields.
- Compute Determinants: The calculator computes the determinant of the coefficient matrix ( D ) and the determinants ( D_i ) for each variable.
- Solve for Variables: Using the formula ( x_i = \frac{D_i}{D} ), the calculator determines the values of the variables.
- Display Solutions: The solutions are presented in a clear, organized manner, often with intermediate steps for educational purposes.
Advantages of Using a Cramer’s Rule Calculator
- Accuracy: Eliminates human errors in determinant calculations.
- Efficiency: Saves time, especially for larger systems.
- Educational Value: Provides step-by-step solutions, aiding in understanding the method.
- Versatility: Can handle systems of any size, within computational limits.
Implementation and Features
A well-designed Cramer’s Rule Calculator should include the following features:
Step-by-Step Solution
Break down the solution process, showing each determinant calculation and the final division to find x_i .
Pros and Cons
- Pros: Analytical solutions, educational, handles any system size (theoretically).
- Cons: Computationally expensive for large systems, requires non-zero determinant.
Expert Insight
While Cramer's Rule is theoretically powerful, it is rarely used in practice for large systems due to its O(n!) complexity. Numerical methods like Gaussian elimination or LU decomposition are preferred for efficiency.
Practical Applications
Cramer’s Rule, facilitated by a calculator, finds applications in:
- Engineering: Solving systems of equations in circuit analysis or structural mechanics.
- Economics: Analyzing supply and demand models.
- Physics: Solving systems derived from physical laws.
- Education: Teaching linear algebra concepts in a tangible way.
Example Usage
Consider the system:
[ \begin{cases} 2x + 3y = 8 \ 4x - 2y = 2 \end{cases} ]
A Cramer’s Rule Calculator would:
- Compute ( D = \det\begin{pmatrix} 2 & 3 \ 4 & -2 \end{pmatrix} = (2)(-2) - (3)(4) = -4 - 12 = -16 ).
- Compute ( D_x = \det\begin{pmatrix} 8 & 3 \ 2 & -2 \end{pmatrix} = (8)(-2) - (3)(2) = -16 - 6 = -22 ).
- Compute ( D_y = \det\begin{pmatrix} 2 & 8 \ 4 & 2 \end{pmatrix} = (2)(2) - (8)(4) = 4 - 32 = -28 ).
- Find ( x = \frac{D_x}{D} = \frac{-22}{-16} = \frac{11}{8} ) and ( y = \frac{D_y}{D} = \frac{-28}{-16} = \frac{7}{4} ).
Conclusion
A Cramer’s Rule Calculator is an indispensable tool for anyone working with systems of linear equations. It combines the theoretical elegance of Cramer’s Rule with the practical efficiency of modern computing, making it an essential resource in both educational and professional settings. Whether for learning, verification, or application, such a calculator simplifies the process of finding solutions, ensuring accuracy and saving valuable time.
Key Takeaway
Cramer's Rule, when implemented via a calculator, offers a precise and educational approach to solving linear systems, though its practical use is limited to small systems due to computational constraints.
What is Cramer’s Rule used for?
+Cramer’s Rule is used to solve systems of linear equations by expressing the solutions in terms of ratios of determinants. It is particularly useful for small systems and educational purposes.
Can Cramer’s Rule handle non-square systems?
+No, Cramer’s Rule applies only to square systems (same number of equations and variables) with a non-zero determinant.
Why is Cramer’s Rule inefficient for large systems?
+Cramer’s Rule involves computing determinants, which have a factorial time complexity ( O(n!) ), making it impractical for large systems.
What are alternatives to Cramer’s Rule?
+Alternatives include Gaussian elimination, LU decomposition, and iterative methods like the Jacobi or Gauss-Seidel methods, which are more efficient for larger systems.
How does a Cramer’s Rule Calculator work?
+The calculator automates determinant calculations and applies Cramer’s Rule formula to find solutions, displaying intermediate steps for clarity.



