All Properties In Math

The Comprehensive Guide to Mathematical Properties: A Deep Dive into the Foundations of Mathematics
Mathematics is built upon a set of fundamental properties that govern the behavior of numbers, operations, and functions. These properties are the building blocks of mathematical reasoning, enabling us to solve complex problems, prove theorems, and develop new theories. In this article, we’ll embark on a journey through the vast landscape of mathematical properties, exploring their definitions, applications, and interconnections.
Arithmetic Properties: The Foundation of Number Theory
1. Commutative Property

- Addition: a + b = b + a
- Multiplication: a × b = b × a
This property is fundamental in arithmetic, allowing us to rearrange terms and simplify expressions.
2. Associative Property
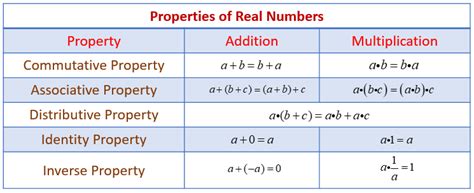
- Addition: (a + b) + c = a + (b + c)
- Multiplication: (a × b) × c = a × (b × c)
This property enables us to perform operations in any order, facilitating complex calculations.
3. Distributive Property
- a × (b + c) = a × b + a × c
This property is essential in algebra, allowing us to expand and simplify expressions.
Algebraic Properties: The Language of Equations
4. Identity Property
- Additive Identity: a + 0 = a
- Multiplicative Identity: a × 1 = a
These identities serve as reference points, simplifying expressions and equations.
5. Inverse Property

- Additive Inverse: a + (-a) = 0
- Multiplicative Inverse: a × (1/a) = 1
This property is crucial in solving equations and performing operations.
Geometric Properties: The Characteristics of Shapes
6. Symmetry Property
- Reflection: Mirroring a shape across a line
- Rotation: Turning a shape around a point
- Translation: Sliding a shape without rotating or reflecting it
Symmetry is a fundamental concept in geometry, appearing in various forms, including line symmetry, rotational symmetry, and point symmetry.
Calculus Properties: The Behavior of Functions
7. Continuity Property
- lim(x → a) f(x) = f(a)
Continuity is essential in calculus, enabling us to apply theorems, calculate limits, and analyze function behavior.
8. Differentiability Property
- Calculate slopes and tangents
- Analyze function behavior and curvature
- Apply optimization techniques
9. Commutative Property of Set Intersection and Union
- Intersection: A ∩ B = B ∩ A
- Union: A ∪ B = B ∪ A
This property enables us to manipulate sets and perform operations in any order.
10. Associative Property of Set Intersection and Union
- Intersection: (A ∩ B) ∩ C = A ∩ (B ∩ C)
- Union: (A ∪ B) ∪ C = A ∪ (B ∪ C)
This property facilitates complex set operations and manipulations.
Number Theory Properties: The Characteristics of Integers
11. Divisibility Property
- Factorize integers
- Analyze prime numbers
- Study Diophantine equations
Frequently Asked Questions (FAQ)
What is the difference between the commutative and associative properties?
+The commutative property concerns the order of operands, while the associative property deals with the grouping of operands. In other words, the commutative property allows us to rearrange terms (e.g., a + b = b + a), whereas the associative property enables us to group terms (e.g., (a + b) + c = a + (b + c)).
Why are mathematical properties important?
+Mathematical properties provide a foundation for mathematical reasoning, enabling us to solve complex problems, prove theorems, and develop new theories. They ensure consistency, simplify calculations, and facilitate the application of mathematical concepts across various domains.
How do geometric properties relate to symmetry?
+Geometric properties, such as symmetry, describe the characteristics of shapes and their behavior under transformations. Symmetry, in particular, refers to the property of a shape remaining unchanged under specific transformations, such as reflection, rotation, or translation.
What is the role of the distributive property in algebra?
+The distributive property bridges the gap between addition and multiplication, allowing us to expand and simplify expressions. It states that a × (b + c) = a × b + a × c, enabling us to break down complex expressions into simpler components.
How do calculus properties, such as continuity and differentiability, impact function analysis?
+Calculus properties like continuity and differentiability provide insights into function behavior, enabling us to calculate limits, analyze slopes and tangents, and apply optimization techniques. These properties are essential for understanding the characteristics of functions and their applications in various fields.
Conclusion: The Interconnected Web of Mathematical Properties
Mathematical properties form an intricate web, interconnecting various branches of mathematics and providing a foundation for mathematical reasoning. From arithmetic and algebra to geometry, calculus, and number theory, these properties enable us to explore the complexities of the mathematical universe. By understanding and applying these properties, we can unlock new insights, solve complex problems, and push the boundaries of human knowledge.
As we’ve seen, mathematical properties are not isolated concepts but rather interconnected threads that weave together the fabric of mathematics. By studying and appreciating these properties, we can develop a deeper understanding of the mathematical world and its applications in science, engineering, and beyond.
Final Thought: Mathematics is a vast and ever-evolving field, with new properties and relationships waiting to be discovered. As we continue to explore the mathematical landscape, we’ll undoubtedly uncover new connections, patterns, and insights that will shape our understanding of the world and its complexities.



